Calculus II - Center of Mass

Show Mobile Notice Show All Notes Hide All Notes

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 8.3 : Center Of Mass

In this section we are going to find the center of mass or centroid of a thin plate with uniform density $\rho $. The center of mass or centroid of a region is the point in which the region will be perfectly balanced horizontally if suspended from that point.

So, let’s suppose that the plate is the region bounded by the two curves $f\left( x \right)$ and $g\left( x \right)$ on the interval $\left[ {a,b} \right]$. So, we want to find the center of mass of the region below.

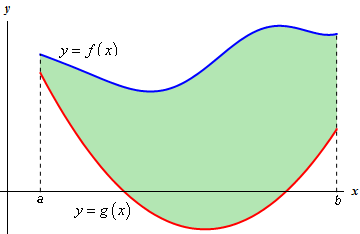
This is the graph of two unknown functions on the domain a<x<b that are mostly in the 1st quadrant. The graph of f(x) is always over the graph of g(x) and the graph of g(x) dips briefly into the 4th quadrant just to make the point that the quadrant we are in does not matter. The area between the two functions has been shaded in.

We’ll first need the mass of this plate. The mass is,

\[\begin{align*}M & = \rho \left( {{\mbox{Area of plate}}} \right)\\ & = \rho \int_{{\,a}}^{{\,b}}{{f\left( x \right) - g\left( x \right)\,dx}}\end{align*}\]

Next, we’ll need the moments of the region. There are two moments, denoted by ${M_x}$ and ${M_y}$. The moments measure the tendency of the region to rotate about the $x$ and $y$-axis respectively. The moments are given by,

Equations of Moments

\[\begin{align*}{M_x} & = \rho \int_{{\,a}}^{{\,b}}{{\frac{1}{2}\left( {{{\left[ {f\left( x \right)} \right]}^2} - {{\left[ {g\left( x \right)} \right]}^2}} \right)\,dx}}\\ {M_y} & = \rho \int_{{\,a}}^{{\,b}}{{x\left( {f\left( x \right) - g\left( x \right)} \right)\,dx}}\end{align*}\]

The coordinates of the center of mass, $\left( {\overline{x},\overline{y}} \right)$, are then,

Center of Mass Coordinates

\[\begin{align*}\overline{x} & = \frac{{{M_y}}}{M} = \frac{{\int_{{\,a}}^{{\,b}}{{x\left( {f\left( x \right) - g\left( x \right)} \right)\,dx}}}}{{\int_{{\,a}}^{{\,b}}{{f\left( x \right) - g\left( x \right)\,dx}}}} = \frac{1}{A}\int_{{\,a}}^{{\,b}}{{x\left( {f\left( x \right) - g\left( x \right)} \right)\,dx}}\\ \overline{y} & = \frac{{{M_x}}}{M} = \frac{{\int_{{\,a}}^{{\,b}}{{\frac{1}{2}\left( {{{\left[ {f\left( x \right)} \right]}^2} - {{\left[ {g\left( x \right)} \right]}^2}} \right)\,dx}}}}{{\int_{{\,a}}^{{\,b}}{{f\left( x \right) - g\left( x \right)\,dx}}}} = \frac{1}{A}\int_{{\,a}}^{{\,b}}{{\frac{1}{2}\left( {{{\left[ {f\left( x \right)} \right]}^2} - {{\left[ {g\left( x \right)} \right]}^2}} \right)\,dx}}\end{align*}\]

where,

\[A = \int_{{\,a}}^{{\,b}}{{f\left( x \right) - g\left( x \right)\,dx}}\]

Note that the density, $\rho $, of the plate cancels out and so isn’t really needed.

Let’s work a couple of examples.

Example 1 Determine the center of mass for the region bounded by $y = 2\sin \left( {2x} \right)$, $y = 0$ on the interval $\left[ {0,\displaystyle \frac{\pi }{2}} \right]$.

Show Solution

Here is a sketch of the region with the center of mass denoted with a dot.

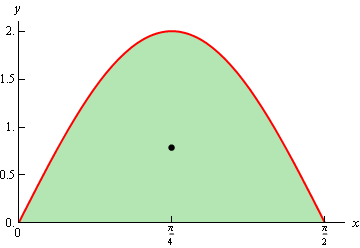
$This is the graph of $y=2\sin \left( 2x \right)$ on the domain 0<x<$\frac{\pi}{2}$ and the area between the curve and the x-axis is shaded. There is also a dot at the center of mass whose coordinates will be determined below.$

Let’s first get the area of the region.

\[\begin{align*}A & = \int_{{\,0}}^{{\,\frac{\pi }{2}}}{{2\sin \left( {2x} \right)\,dx}}\\ & = \left. { - \cos \left( {2x} \right)} \right|_0^{\frac{\pi }{2}}\\ & = 2\end{align*}\]

Now, the moments (without density since it will just drop out) are,

\[\begin{array}{*{20}{c}}\begin{aligned}{M_x} & = \int_{{\,0}}^{{\,\frac{\pi }{2}}}{{2{{\sin }^2}\left( {2x} \right)\,dx}}\\ & = \int_{{\,0}}^{{\,\frac{\pi }{2}}}{{1 - \cos \left( {4x} \right)\,dx}}\\ & = \left. {\left( {x - \frac{1}{4}\sin \left( {4x} \right)} \right)} \right|_0^{\frac{\pi }{2}}\\ & = \frac{\pi }{2}\end{aligned}& \hspace{0.5in} &\begin{aligned}{M_y} & = \int_{{\,0}}^{{\,\frac{\pi }{2}}}{{2x\sin \left( {2x} \right)\,dx}}\hspace{0.25in}{\mbox{integrating by parts}}...\\ & = - \left. {x\cos \left( {2x} \right)} \right|_0^{\frac{\pi }{2}} + \int_{{\,0}}^{{\,\frac{\pi }{2}}}{{\cos \left( {2x} \right)\,dx}}\\ & = - \left. {x\cos \left( {2x} \right)} \right|_0^{\frac{\pi }{2}} + \left. {\frac{1}{2}\sin \left( {2x} \right)} \right|_0^{\frac{\pi }{2}}\\ & = \frac{\pi }{2}\end{aligned}\end{array}\]

The coordinates of the center of mass are then,

\[\begin{align*}\overline{x} & = \frac{{{}^{\pi }/{}_{2}}}{2} = \frac{\pi }{4}\\ \overline{y} & = \frac{{{}^{\pi }/{}_{2}}}{2} = \frac{\pi }{4}\end{align*}\]

Again, note that we didn’t put in the density since it will cancel out.

So, the center of mass for this region is $\left( {\frac{\pi }{4},\frac{\pi }{4}} \right)$.

Example 2 Determine the center of mass for the region bounded by $y = {x^3}$ and $y = \sqrt x $.

Show Solution

The two curves intersect at $x = 0$ and $x = 1$ and here is a sketch of the region with the center of mass marked with a box.

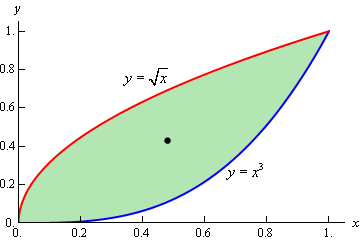
$This is the graph of $y={{x}^{3}}$ and $y=\sqrt{x}$ on the domain 0<x<1. The graph of $y=\sqrt{x}$ is always larger than the graph of $y={{x}^{3}}$ and the area between the curves is shaded. There is also a dot at the center of mass whose coordinates will be determined below.$

We’ll first get the area of the region.

\[\begin{align*}A & = \int_{{\,0}}^{{\,1}}{{\sqrt x - {x^3}\,dx}}\\ & = \left. {\left( {\frac{2}{3}{x^{\frac{3}{2}}} - \frac{1}{4}{x^4}} \right)} \right|_0^1\\ & = \frac{5}{{12}}\end{align*}\]

Now the moments, again without density, are

\[\begin{array}{*{20}{c}}\begin{aligned}{M_x} & = \int_{{\,0}}^{{\,1}}{{\frac{1}{2}\left( {x - {x^6}} \right)\,dx}}\\ & = \left. {\frac{1}{2}\left( {\frac{1}{2}{x^2} - \frac{1}{7}{x^7}} \right)} \right|_0^1\\ & = \frac{5}{{28}} \\ & \end{aligned}& \hspace{0.5in} &\begin{aligned}{M_y} & = \int_{{\,0}}^{{\,1}}{{x\left( {\sqrt x - {x^3}} \right)\,dx}}\\ & = \int_{{\,0}}^{{\,1}}{{{x^{\frac{3}{2}}} - {x^4}\,dx}}\\ & = \left. {\left( {\frac{2}{5}{x^{\frac{5}{2}}} - \frac{1}{5}{x^5}} \right)} \right|_0^1\\ & = \frac{1}{5}\end{aligned}\end{array}\]

The coordinates of the center of mass is then,

\[\begin{align*}\overline{x} & = \frac{{{1}/{5}\;}}{{{5}/{{12}}\;}} = \frac{{12}}{{25}}\\ \overline{y} & = \frac{{{5}/{{28}}\;}}{{{5}/{{12}}\;}} = \frac{3}{7}\end{align*}\]

The coordinates of the center of mass are then,$\left( {\frac{{12}}{{25}},\frac{3}{7}} \right)$.