Section 4.13 : Newton's Method
6. Use Newton’s Method to find all the roots of \(2 - {x^2} = \sin \left( x \right)\) accurate to six decimal places.
Show All Steps Hide All Steps
First, recall that Newton’s Method solves equation in the form \(f\left( x \right) = 0\) and so we’ll need move everything to one side. Doing this gives,
\[f\left( x \right) = 2 - {x^2} - \sin \left( x \right)\]Note that we could have just as easily gone the other direction. All that would have done was change the signs on the function and derivative evaluations in the work below. The final answers however would not be changed.
Next, we are not given a starting value, \({x_{\,0}}\) and unlike Problems 3 & 4 above we are not even given an interval to use as a way to determine a good possible value of \({x_{\,0}}\). We are also not even told how many roots we need to find.
So, to estimate the number of roots of the equation let’s take a look at each side of the equation and realize that each root will in fact be the point of intersection of the two curves on the left and right of the equal sign.
The left side of the original equation is a quadratic that will have its vertex at \(x = 2\) and open downward while the right side is the sine function. Given what we know of these two functions we should expect there to be at most two roots where the quadratic, on its way down, intersects with the sine function. Because the quadratic will never turn around and start moving back upwards it should never intersect with the sine function again after those points.
So, let’s graph both the quadratic and sine function to see if our intuition on this is correct. Doing this gives,
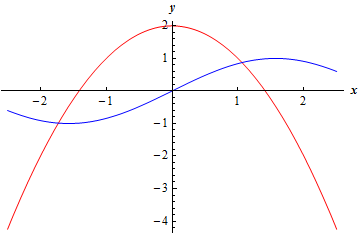
So, it looks like we guessed correctly and should have two roots here.
For each root we’ll use the graph to pick a value of \({x_{\,0}}\) that is close to the root we are after (we’ll go from left to right for the problem) and then run through Newton’s Method,
\[{x_{n + 1}} = {x_n} - \frac{{f\left( {{x_n}} \right)}}{{f'\left( {{x_n}} \right)}}\]until the answers agree to six decimal places.
Note as well that unlike Problems 3 & 4 we are not going to put in all the function evaluations for this problem. We’ll leave that to you to check and verify our final answers for each iteration.
Also note that the analysis that we had to do to estimate the number of roots is something that does need to be done for these kinds of problems and it will differ for each equation. However, if you do have a basic knowledge of how most of the basic functions behave you can do this for most equations you’ll be asked to deal with.
Show Step 2For the left most root let’s start with \({x_{\,0}} = - 1.5\). Here are the results of iterating through Newton’s Method for this root.
\[\begin{align*}{x_{\,1}} & = {x_{\,0}} - \frac{{f\left( {{x_{\,0}}} \right)}}{{f'\left( {{x_{\,0}}} \right)}} = - 1.755181948 & \hspace{0.5in} & {\mbox{No decimal places agree}}\\ {x_{\,2}} & = {x_{\,1}} - \frac{{f\left( {{x_{\,1}}} \right)}}{{f'\left( {{x_{\,1}}} \right)}} = - 1.728754674 & \hspace{0.5in} & {\mbox{Accurate to one decimal place}}\\ {x_{\,3}} & = {x_{\,2}} - \frac{{f\left( {{x_{\,2}}} \right)}}{{f'\left( {{x_{\,2}}} \right)}} = - 1.728466353 & \hspace{0.5in} & {\mbox{Accurate to three decimal places}}\\ {x_{\,4}} & = {x_{\,3}} - \frac{{f\left( {{x_{\,3}}} \right)}}{{f'\left( {{x_{\,3}}} \right)}} = - 1.728466319 & \hspace{0.5in} & {\mbox{Accurate to seven decimal places}}\end{align*}\]So, it looks like the estimate of the left most root is : \(\require{bbox} \bbox[2pt,border:1px solid black]{{x \approx - 1.728466319}}\).
Show Step 3For the right most root let’s start with \({x_{\,0}} = 1\). Here are the results of iterating through Newton’s Method for this root.
\[\begin{align*}{x_{\,1}} & = {x_{\,0}} - \frac{{f\left( {{x_{\,0}}} \right)}}{{f'\left( {{x_{\,0}}} \right)}} = 1.062405571 & \hspace{0.5in} & {\mbox{No decimal places agree}}\\ {x_{\,2}} & = {x_{\,1}} - \frac{{f\left( {{x_{\,1}}} \right)}}{{f'\left( {{x_{\,1}}} \right)}} = 1.061549933 & \hspace{0.5in} & {\mbox{Accurate to two decimal places}}\\ {x_{\,3}} & = {x_{\,2}} - \frac{{f\left( {{x_{\,2}}} \right)}}{{f'\left( {{x_{\,2}}} \right)}} = 1.061549775 & \hspace{0.5in} & {\mbox{Accurate to six decimal places}}\end{align*}\]So, it looks like the estimate of the right most root is : \(\require{bbox} \bbox[2pt,border:1px solid black]{{x \approx 1.061549775}}\).
Show Step 4Using computational aids we found that the actual roots of this equation to be,
\[x = - 1.72846631899718\hspace{0.5in}x = 1.06154977463138\]Note that these weren’t actually asked for in the problem and are only given for comparison purposes.
As a final warning about Newton’s Method, be careful to not assume that you’ll get six (or better in some cases) decimal places of accuracy with just a few iterations.
These problems were chosen with the understanding that it would only take a few iterations of the method. There are problems and/or choices of \({x_{\,0}}\) for which it will take significantly more iterations to get any kind of real accuracy, provided the method even works for that equation and/or choice of \({x_{\,0}}\). Recall that we saw an example in the notes in which the method failed spectacularly.