Section 4.8 : Optimization
4. We are going to fence in a rectangular field. If we look at the field from above the cost of the vertical sides are $10/ft, the cost of the bottom is $2/ft and the cost of the top is $7/ft. If we have $700 determine the dimensions of the field that will maximize the enclosed area.
Show All Steps Hide All Steps
Start SolutionThe first step is to do a quick sketch of the problem. We could probably skip the sketch in this case, but that is a really bad habit to get into. For many of these problems a sketch is really convenient and it can be used to help us keep track of some of the important information in the problem and to “define” variables for the problem.
Here is the sketch for this problem.
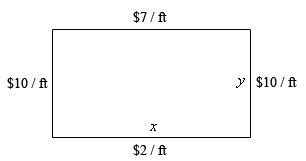
Next, we need to set up the constraint and equation that we are being asked to optimize.
We are told that we have $700 to spend and so the cost of the material will be the constraint for this problem. The cost for the material is then,
\[700 = 10y + 2x + 10y + 7x = 20y + 9x\]We are being asked to maximize the area so that equation is,
\[A = xy\] Show Step 3Now, let’s solve the constraint for \(y\) (that looks like it will only have one fraction in it and so may be “easier”…).
\[y = 35 - \frac{9}{20}x\]Plugging this into the area formula gives,
\[A\left( x \right) = x\left( {35 - \frac{9}{20}x} \right) = 35x - \frac{9}{20}{x^2}\] Show Step 4Finding the critical point(s) for this shouldn’t be too difficult at this point so here is that work.
\[A'\left( x \right) = 35 - \frac{9}{10}x\hspace{0.5in} \to \hspace{0.5in}35 - \frac{9}{10}x = 0\hspace{0.5in} \to \hspace{0.5in}x = \frac{350}{9}\] Show Step 5The second derivative of the area function is,
\[A''\left( x \right) = - \frac{9}{10}\]From this we can see that the second derivative is always negative and so \(A\left( x \right)\) will always be concave down and so the single critical point we got in Step 4 must be a relative maximum and hence must be the value that gives a maximum area.
Show Step 6Now, let’s finish the problem by getting the second dimension.
\[y = 35 - \frac{9}{20}\left( \frac{350}{9} \right) = \frac{35}{2}\]The final dimensions are then,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{x = \frac{350}{9}\hspace{0.5in}y = \frac{35}{2}}}\]