Section 8.3 : Center Of Mass
2. Find the center of mass for the region bounded by y=3−e−x, the x-axis, x=2 and the y-axis.
Show All Steps Hide All Steps
Start SolutionLet’s start out with a quick sketch of the region, with the center of mass indicated by the dot (the coordinates of this dot are of course to be determined in the final step…..).
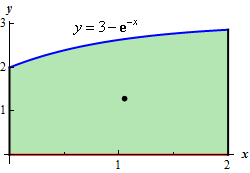
We’ll also need the area of this region so let’s find that first.
A=∫203−e−xdx=(3x+e−x)|20=5+e−2 Show Step 2Next, we need to compute the two moments. We didn’t include the density in the computations below because it will only cancel out in the final step.
Mx=∫2012(3−e−x)2dx=∫2012(9−6e−x+e−2x)dx=12(9x+6e−x−12e−2x)|20=254+3e−2−14e−4My=∫20x(3−e−x)dx=∫203x−xe−xdx=(32x2+xe−x+e−x)|20=5+3e−2For the second term in the My integration we used the following integration by parts.
∫xe−xdxu=xdu=dxdv=e−xdxv=−e−x∫xe−xdx=−xe−x+∫e−xdx=−xe−x−e−x=−(xe−x+e−x)The minus sign here canceled with the minus sign that was in front of the term in the full integral.
Make sure you don’t forget integration by parts! It is a fairly common integration technique for these kinds of problems.
Show Step 3Finally, the coordinates of the center of mass is,
¯x=MyM=ρ(5+3e−2)ρ(5+e−2)=1.05271¯y=MxM=ρ(254+3e−2−14e−4)ρ(5+e−2)=1.29523The center of mass is then : (1.05271,1.29523).